최근 인공지능 기술이 주목받고 있다. 이것은 빅데이터 기술과 사물 인터넷 기술의 발전으로 다양하고 질 좋은 데이터를 손쉽게 수집할 수 있게 되었기 때문이다. 인공지능 기술의 일종인 딥러닝은 데이터 속에 있는 원리를 추론함으로써 이전에는 풀기 어려웠던 문제들을 풀 수 있게 만들었다. 대표적으로 이미지 분류, 자연어 처리, 영상처리 등의 분야에서 기존의 알고리즘보다 훨씬 뛰어난 성능을 보인다. 또한 알파고는 알고리즘이 아직은 넘을 수 없는 벽이라 여겼던 바둑에서 인간을 이겼다. 이처럼 딥러닝은 다양한 분야에서 활용되고 있다. 본 기초강좌에서는 딥러닝 이론에 대한 기본 개념을 소개함으로써, 딥러닝 기법에 관심이 있거나 필요한 연구자들에게 도움이 되고자 한다.
- 기계학습과 딥러닝에 대한 개괄적 이해
인공지능은 컴퓨터에게 데이터를 학습시켜 마치 사람처럼 스스로 의사결정을 할 수 있게 한다. 예를 들어, 사진을 보고 무슨 사진인지 구분하도록 하는 분류 모델을 만들기 위해서는 컴퓨터에게 사진을 계속 보여주면서 이 사진은 어떤 것에 대한 것인지에 대한 정답을 학습 시켜주어야 한다. 이런 방식을 ‘지도 기계학습’이라고 부른다. 최근에 뛰어난 성능을 보이며 많은 관심을 받고있는 딥러닝 역시 기계학습과 유사한 방법이다. 딥러닝과 기계학습은 데이터를 이용하여 모델을 학습한다는 공통점이 있지만 데이터를 학습하는 과정에서 큰 차이가 있다. 기계학습으로 이미지를 인식하기 위해서는 사진을 그대로 사용하는 것이 아니라 사진 속에 객체를 가장 잘 구분할 수 있는 특성인자 (feature)를 찾아내야 한다. 기계학습에서 모델의 성능을 결정하는 것은 ‘이 특성인자가 얼마나 데이터를 잘 대표하는가’ 이다. 반면 딥러닝의 경우에는 사람이 특성인자를 선정하는 것이 아니라 데이터에서 모델을 학습하는 과정에서 목표를 잘 달성할 수 있는 특성인자를 스스로 찾는다. 기계분야에서도 복잡한 기계시스템으로부터 취득된 데이터에서 특성인자를 찾아내는 것은 전문가 지식을 많이 요구하기 때문에 기계학습의 적용에 어려움이 많았다. 반면 딥러닝은 특성인자를 자동으로 찾아내기 때문에 기계분야에서 딥러닝을 활용하려는 시도가 늘어나고 있다.
딥러닝은 인간 뇌의 정보처리 과정을 수학적인 모델링을 통해 모사한 모형이다. 따라서 그 바탕에는 복잡한 수학적 배경이 깔려있다. 하지만 이 글에서는 수학적 증명이나 수식을 설명하기 보다는 딥러닝 모델의 구조와 원리에 대해서 설명하도록 하겠다.
- 인공 신경망 (Neural Networks)
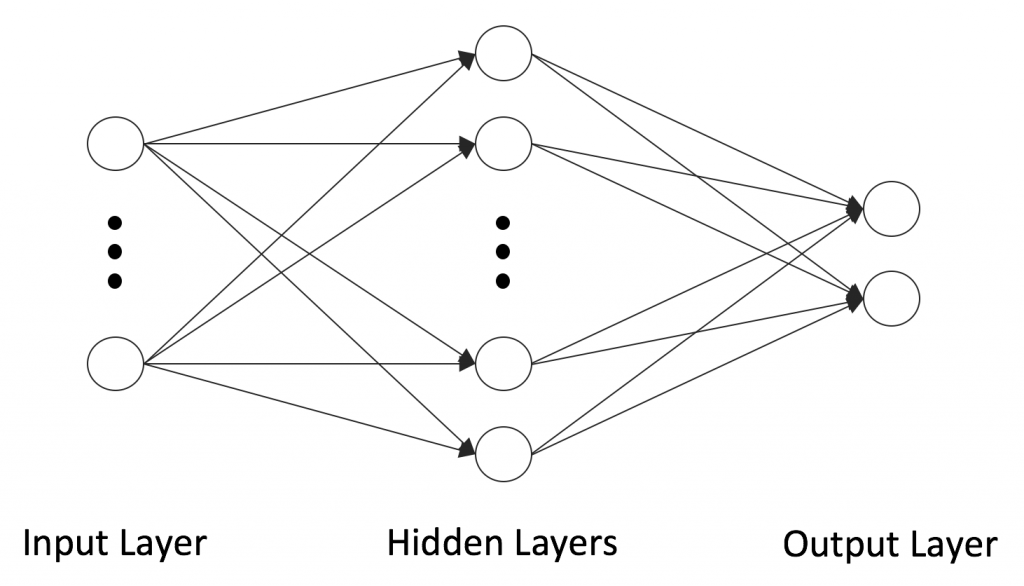
인공 신경망은 생물학의 신경망에서 영감을 얻은 수학적 모델이다. 인공 신경망은 시냅스의 결합으로 네트워크를 형성한 인공 뉴런이 학습을 통해 시냅스의 결합 세기를 변화시켜 문제 해결 능력을 가지고 있는 모델 전반을 가리킨다. 인공 신경망은 과거부터 많이 연구되었으며 역사적으로 오래된 알고리즘이다. 하지만 몇가지 단점으로 인해 잊혀지고 있었던 알고리즘이 2000년대 이후 딥러닝의 출현으로 인공 신경망에 대한 관심이 다시 증가하고 있다. 인공 신경망은 그림1과 같이 일반적으로 입력층 (Input layer), 은닉층 (Hidden layers) 과 출력층 (Output layer)로 구성되어 있으며 각 층에 포함된 뉴런들이 가중치를 통해 연결되어 있다. 가중치와 뉴런 값의 선형 결합과 비선형 활성화 함수 (Activation function)을 통해 인공 신경망은 복잡한 함수를 근사 (Function approximation) 할 수 있는 형태를 가지고 있다.
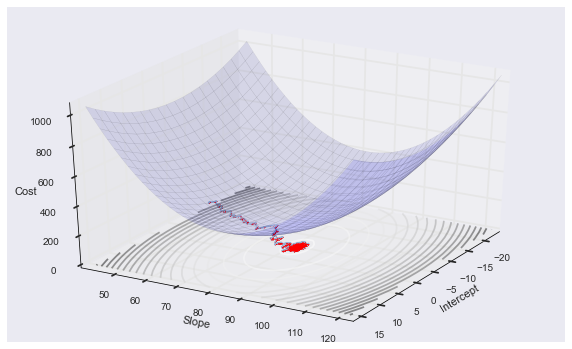
인공 신경망 학습의 목적은 출력층에서 계산된 출력과 실제 출력의 값 차이를 최소화시키는 가중치를 찾는 데 있다. 문제를 해결할 최적의 가중치를 학습하기 위해 인공 신경망에서는 목적 함수 (Object function or loss function)를 정의한다. 목적 함수가 정의되면 가중치의 변화에 따른 오차의 변화를 계산할 수 있기 때문에 오차와 가중치의 관계를 연쇄법칙 (Chain rule)을 이용한 편미분으로 구할 수 있으며, 일반적으로 stochastic gradient descent를 통해 각각의 가중치를 반복적으로 갱신할 수 있다 (그림2). 가중치는 출력층에서부터 입력층까지 역방향으로 갱신되는데 이를 역전파 알고리즘 (Backpropagation)이라고 한다.
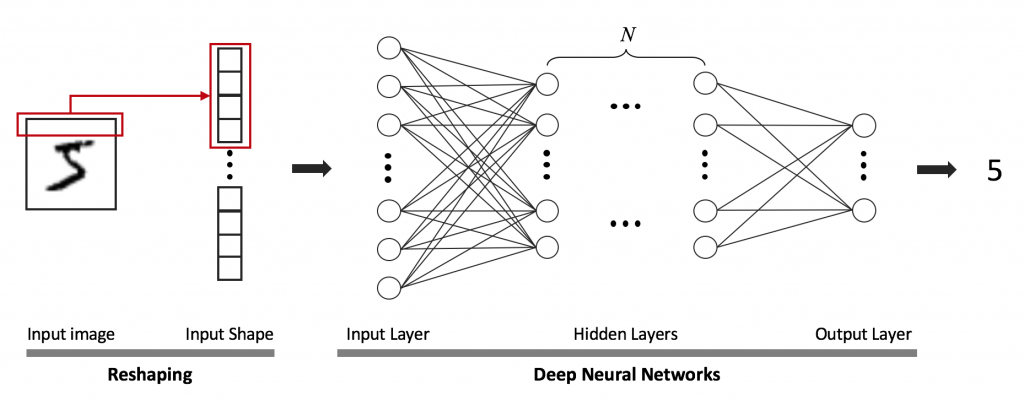
인공 신경망을 이용하기 위해서는 사용자가 모델 구조와 학습데이터만 준비하면 된다. 학습 과정에서 데이터를 가장 잘 표현할 수 있는 특성인자를 자동으로 추출한다. 그림3에서처럼 심층 신경망 (Deep Neural Networks)은 입력층과 출력층 사이에 여러 개의 은닉층들로 이뤄진 인공 신경망이다. 심층 신경망은 많은 은닉층을 통해 복잡한 비선형 관계들을 모델링 할 수 있다. 이처럼 층의 개수를 늘림으로써 고도화된 추상화가 가능한 신경망 구조를 최근엔 딥러닝이라고 부른다 [1]. 하지만 단순히 은닉층의 개수만 늘어난 것뿐만 아니라 최근 관련 연구자들에 의해서 다양한 문제를 해결하기 위한 독특한 구조가 많이 개발되었다. 그 중에서 유명한 합성곱 신경망 (Convolutional Neural Networks), 순환 신경망 (Recurrent Neural Networks), 오토인코더 (Autoencoder)의 구조를 알아보겠다.
- 합성곱 신경망 (Convolutional Neural Networks, CNN)
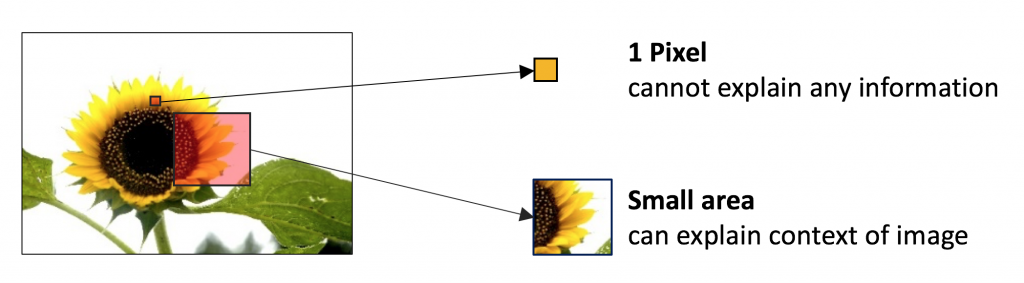
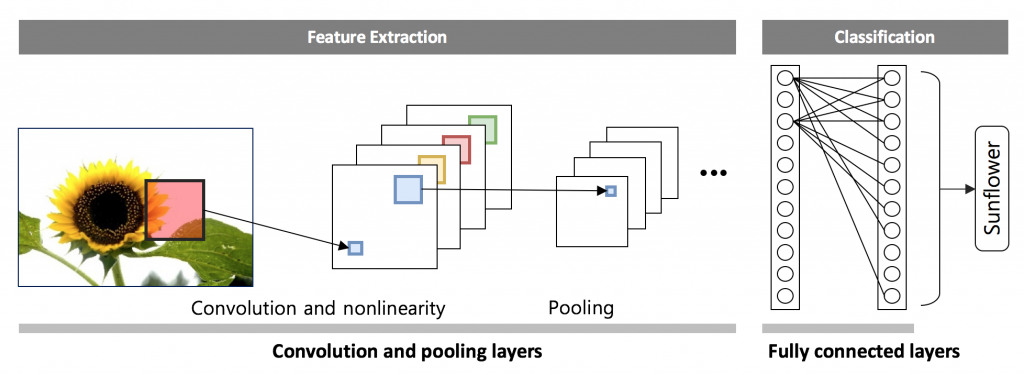
‘백문불여일견’ 이라는 말이 있듯이 이미지는 많은 시각적인 정보를 담고 있다. 따라서 이미지에서 필요한 정보를 추출하고자 하는 노력은 오래 전부터 계속되어 왔다. 특히 영상처리 분야에서는 물체를 대표할 수 있는 꼭지점, 윤곽선과 같은 특성인자 추출을 통한 접근을 시도해왔다. 하지만 최근 딥러닝 중 합성곱 신경망의 등장은 이미지 인식의 패러다임을 바꾸어 놓았다. 인간은 물체를 인지할 때, 이미지의 단위 요소를 수치적으로 이해하기보다는 물체를 종합적 또는 전체적으로 받아드린다. 예를 들어, 해바라기 이미지를 볼 때 픽셀 값 하나하나를 관찰하는 것이 아니라 일정 영역 픽셀들의 유기적인 관계를 통해 해바라기를 인지한다 (그림4). 합성곱 신경망은 인간의 이러한 인지 모델을 수학적으로 표현한 구조이다 [2]. 특성인자를 추출하기 위해서 합성곱 계층 (Convolutional layer)과 통합 계층 (Pooling layer)을 사용하며, 이 특성인자를 일반적인 인공 신경망 (Fully-connected layers)의 입력으로 이용해 이미지를 분류하고 인지한다 (그림5).
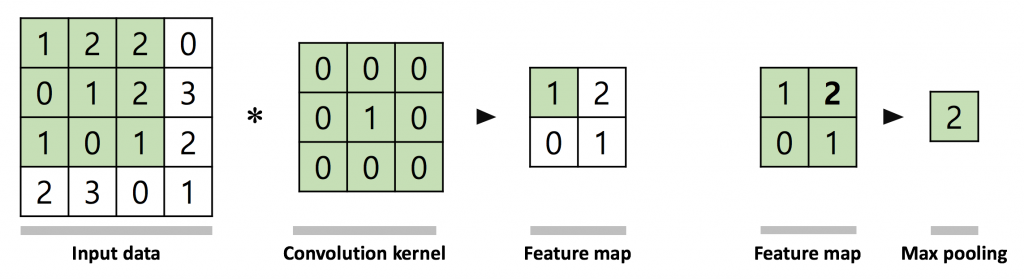
합성곱 계층은 커널을 일정한 간격으로 이동해가며 합성곱 연산을 수행하며, 이는 영상처리분야에서 필터링과 비슷한 과정이다. 합성곱에 사용되는 커널 값은 인공 신경망의 가중치에 해당하기 때문에 데이터로부터 최적의 커널이 학습된다고 볼 수 있다. 통합 계층은 주로 합성곱 계층에서 출력된 데이터의 크기를 줄이기 위해서 사용한다. 통합 계층에는 max-pooling과 average pooling등이 있는데, max-pooling은 해당 영역에서 최대값을 찾는 연산이고 average pooling은 해당 영역의 평균값을 계산하는 연산이다. 합성곱 연산과 마찬가지로 창을 이동하면서 해당 pooling 연산을 수행하며, 이는 특성인자에 공간 불변성 (Spatial invariance)를 더하는 기능으로도 해석된다 (그림6) [3].
- 순차 신경망 (Recurrent Neural Networks, RNN)
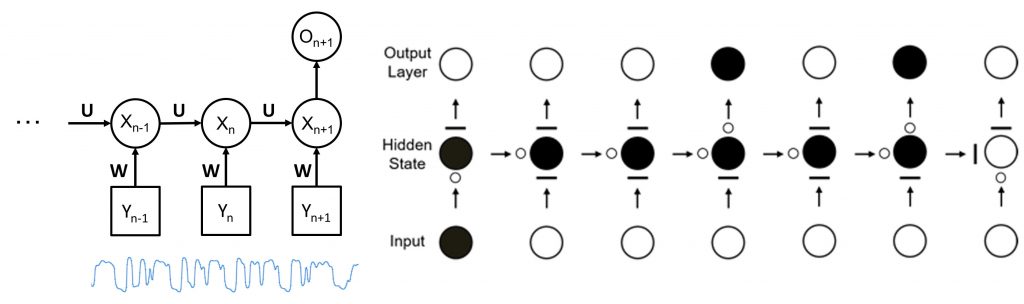
순차 신경망은 심층 신경망의 또 다른 형태 중 하나로, 시계열 데이터에 내제되어 있는 동적 패턴과 특성 파악에 유용하다. 이는 구조적으로 메모리에 해당하는 은닉 상태 (Hidden state)를 통해 과거 정보가 다음 단계로 전달 가능하기 때문이다. 이러한 구조적 특징 때문에, 순차 신경망은 최근 자연어 처리에 뛰어난 성능을 보인다 [4]. 순차 신경망 이전에도 시계열 데이터를 다루기 위한 몇가지 모델이 존재하였다. 가장 잘 알려진 모델로 칼만 필터 (Kalman Filter)와 히든 마르코프 모델 (Hidden Markov Model)이 있는데 이들은 공통적으로 관찰되는 데이터 이면에 실제 상태를 나타내는 은닉 상태가 숨어있다는 가정에서 출발한다 (그림7). 이들 모델은 시계열 데이터를 다루기에 적합하지만 그림 7에서처럼 를 설명하는 선형 시스템 혹은 전이확률행렬 A를 먼저 정의해야 하는 현실적인 어려움이 있다.
기본적으로 순차 신경망 역시 은닉 상태를 이용하여 모델을 구성한다. 하지만 은닉 상태를 정의하는 방식에 있어서 큰 차이가 있다. 그림8 (a)처럼 순차 신경망은 은닉 상태와 입력 데이터, 결과 노드가 연결되어 있는 네트워크로 구성되어 있다. 하지만 은닉 상태를 위한 선형시스템이나 전이확률행렬을 미리 정의해줄 필요 없이 학습 과정에서 은닉 상태들을 동적 행동을 연결하는 전이 행렬 U와 시계열 데이터와 은닉 상태를 연결하는 행렬 W가 구해진다. 순차 신경망은 딥러닝의 특징인 고도의 추상화를 통한 특성인자의 추출이라는 특성을 지님과 동시에 과거의 정보를 기억하는 다수의 은닉 상태를 활용하여 결과적으로 시계열 데이터에 내제되어 있는 동적 패턴과 특성 파악을 위한 모델이라 할 수 있다.
하지만 순차 신경망은 학습과정에서 이전 시간의 은닉 상태 값이 현재 시간의 은닉 상태에 영향을 주기 때문에 학습이 진행됨에 따라 누적 값이 기하급수적으로 증가하거나, 빠르게 0으로 수렴하는 현상이 발생한다. 이를 해결하기 위해 제안된 구조가 그림8 (b)의 Long Short-Term Memory (LSTM) 구조이다. 세개의 게이트와 동적인 정보를 기억하는 메모리를 이용하여 출력 값을 계산함으로써 발산 또는 수렴 문제를 막을 수 있다. 즉, LSTM 구조는 각각의 은닉 상태 정보를 걸러서 중요한 정보만 취득하고 내보내는 형태로 변형시키는 역할을 한다.
- 오토인코더 (Autoencoder)
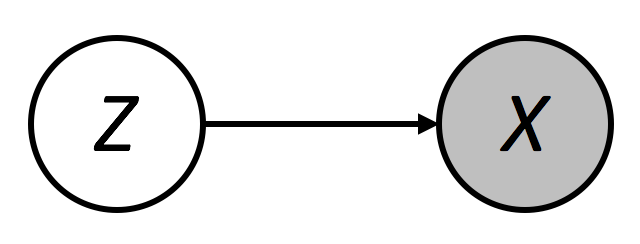
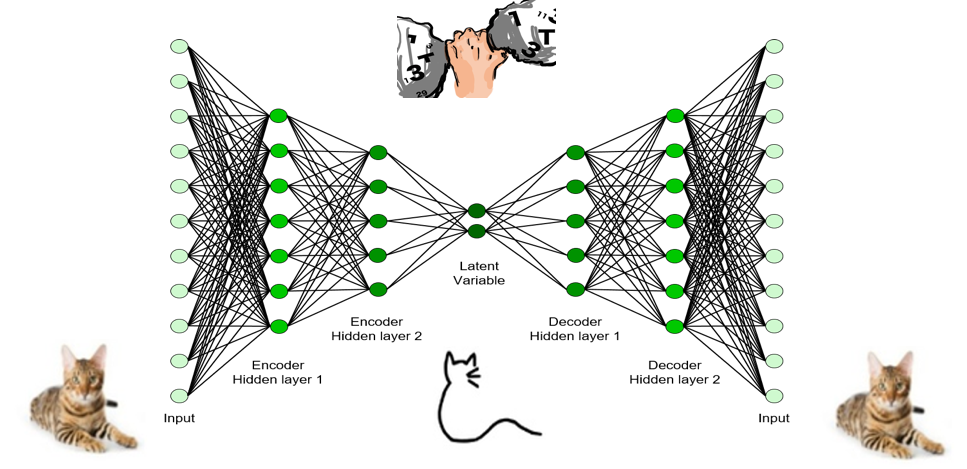
대부분의 복잡한 공학 문제는, 그 문제의 이면에 존재하는 원리를 파악할 수 있으면 의외로 쉬운 문제가 될 때가 있다. 이러한 이유로 복잡한 데이터를 ‘압축’하여 간단히 표현하고자 하는 다양한 노력들이 이루어진다. 그 예로 Singular Value Decomposition (SVD) 혹은 Principal Component Analysis (PCA)가 있으며, 앞서 설명한 순차 신경망 또한 시계열 데이터를 직접적으로 이용하는 것이 아니라 은닉 상태를 추론하여 문제를 풀어 나간다. 은닉 상태를 추론하는 문제는 라벨이 필요하지 않기 때문에 비지도학습으로 분류되며, 그림9과 같이 입력 데이터 X 의 이면에 존재하는 보다 낮은 차원의 Z를 추론하는 방식이다.
그림10 (a)와 같이 도식화된 병목 구조를 가지고 출력과 입력이 같을 때 신경망 학습을 고려해보자. 이러한 구조에서는 반드시 1) 정보를 압축하는 인코더를, 2) 압축된 정보를 바탕으로 데이터를 복원하는 디코더를 학습해야한다. 이러한 아이디어를 바탕으로 그림10 (b)과 같은 심층 신경망 오토인코더를 설계할 수 있다. 병목에서의 값들을 입력신호의 압축된 정보로 해석할 수 있다. 오토인코더의 인코더를 이용하여 데이터의 차원 축소가 가능하다. 이미지와 같이 높은 차원에 존재하는 데이터를 저차원으로 표현할 수 있으며, 축소된 공간에서 분류도 수행 할 수 있다. 반면, 오토인코더의 디코더를 이용하면 축소된 공간에서 임의의 점에 해당하는 가상의 데이터를 원공간에서 생성해낼 수 있다. 결함 데이터가 일반적으로 부족한 고장진단 분야의 경우 (데이터 불평형 문제), 축소된 공간에서의 고장분포를 파악하여 이에 해당하는 다양한 고장데이터를 가상으로 생성할 때 사용할 수 있다. 이밖에도 정보를 압축하고 복원하는 구조로 Convolutional layer를 통한 오토인코더 방법 (Convolutional Autoencoder), 베이지안적 사고를 바탕으로 신경망을 최적화 시키는 방법 (Variational Autoencoder) 등이 제안되었다 [5, 6].
- 맺음말
인공 신경망은 기존의 기계학습 접근방법에서 요구되었던 엔지니어의 지식기반 특성인자 추출을 자동화, 심층화 함으로써 기존에 존재하던 데이터 기반의 기계학습 알고리즘의 한계를 상당히 극복하였다. 본 기초강좌에서는 데이터 형태에 따른 기본적인 심층 신경망의 구조를 살펴보았다. 합성곱 신경망을 통하여 이미지 데이터 분석, 순환 신경망을 통하여 시계열 데이터 분석이 가능하다. 또한 오토인코더를 이용하여 다양한 형태의 데이터 차원 축소와 가상 데이터 생성이 가능하다. 이러한 이미지 데이터와 시계열 데이터는 소음진동 분야에서도 자주 사용되는 형태의 데이터이기 때문에 딥러닝 적용 가능성도 높다고 할 수 있다.
본 글의 딥러닝에 대한 기초적인 소개를 통해 소음진동분야의 다양한 구성원들이 각자의 연구에 이를 활용하여 산업 전체의 혁신을 가져오기를 기대한다. 가까운 미래에는 기존에 기계학습 방법으로 어려웠던 다양한 기계 및 제조 산업의 문제들을 딥러닝을 통해 극복하는 ‘Deep Manufacturing’의 시대가 오기를 기대하며 글을 마무리한다.
(인공신경망/합성곱신경망/순환신경망의 구현을 위한 파이썬 텐서플로우 코드는 http://isystems.unist.ac.kr/ 에서 확인할 수 있습니다.)
김수현, 울산과학기술원, 제어설계공학과, 석사과정, kimsh12191@unist.ac.kr
박승태, 울산과학기술원, 제어설계공학과, 석사과정, swash21@unist.ac.kr
정해동, 울산과학기술원, 제어설계공학과, 박사과정, hdhd13@unist.ac.kr
이승철, 울산과학기술원, 제어설계공학과, 조교수, seunglee@unist.ac.kr
<본 콘텐츠는 2017년도 5월호 [소음진동]에 ‘딥 러닝(Deep Learning)’이라는 제목으로 실린 것입니다.>
※ 참고 문헌
- LeCun, Y., Bengio, Y., and Hinton, G., 2015, Deep Learning, Nature, 521(7553), 436-444.
- LeCun, Y., and Bengio, Y, 1995, Convolutional Networks for Images, Speech, and Time Series, The Handbook of Brain Theory and Neural Networks, 3361(10).
- Jeong, H., Park, S., Woo, S., and Lee, S., 2016, Rotating Machinery Diagnostics Using Deep Learning on Orbit Plot Images, Procedia Manufacturing, 5, 1107-1118.
- Graves, A., Mohamed, A. R., and Hinton, G., 2013, Speech Recognition with Deep Recurrent Neural Networks, In Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on, pp. 6645-6649.
- Noh, H., Hong, S., and Han, B., 2015, Learning Deconvolution Network for Semantic Segmentation, In Proceedings of the IEEE International Conference on Computer Vision, pp. 1520-1528.
- Kingma, D. P., and Welling, M., 2013, Auto-encoding Variational Bayes, arXiv preprint arXiv:1312.6114.